superrific
Master of the ZZLverse
- Messages
- 11,231
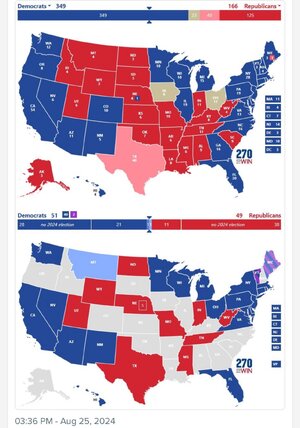
1. It depends on why she loses PA. If it's a state specific thing, then arguably she might be able to offset that loss with NC or GA. There's no inherent reason why she can't win either of those states. They have a bigger R partisan lean than PA, but again, if the PA thing is state-specific (i.e. fracking), then it's not game over.Her recent polling in PA has not been good, which is a major concern. It’s pretty much all she wrote if she loses PA.
There are many paths to victory with PA. Almost none without it. And I’m highly skeptical that GA or NC actually go blue in this election.
The campaign has to be laser focused on PA until Election Day.
2. If she wins PA, she's very likely to take MI and WI and that's pretty much all she needs.
3. And we get another idiocy of the electoral college. AZ + NV is enough to make up the loss of MI. It's not enough to make up the loss of PA. Does that make sense? I mean, I guess PA has more people than MI but it's not really about the population. It's about the arithmetic. It just so happens that the 4 EVs make a difference this go round, primarily because the Dems are winning VA instead of NC and because Utah just barely squeezed ahead of MN for the last EV.
And all of this, even though the vote margin would probably be the same in Michigan as Pennsylvania -- and proportionally bigger in MI. So it's better for Kamala to do better in PA than MI, even if she does worse in the two put together. It is so frustrating.
4. I still can't believe that there is no appetite in half the country to get rid of the EC. I get it -- ideology. But there's no reason that the GOP can't win in a non-EC world. They might need to tweak their policies a bit, and make more of an effort in CA, but it's doable. Meanwhile, the vast majority of the citizens in this country actually have no say at all about the next president, because only PA, MI, WI, NC and AZ matter (and not all of them do).
Every election boils down to four or five swing states. A constitutional amendment can pass with 38 states approving. It would undoubtedly be better for the 45 non-swing states to get rid of the EC and make their votes matter. And yet. And yet.